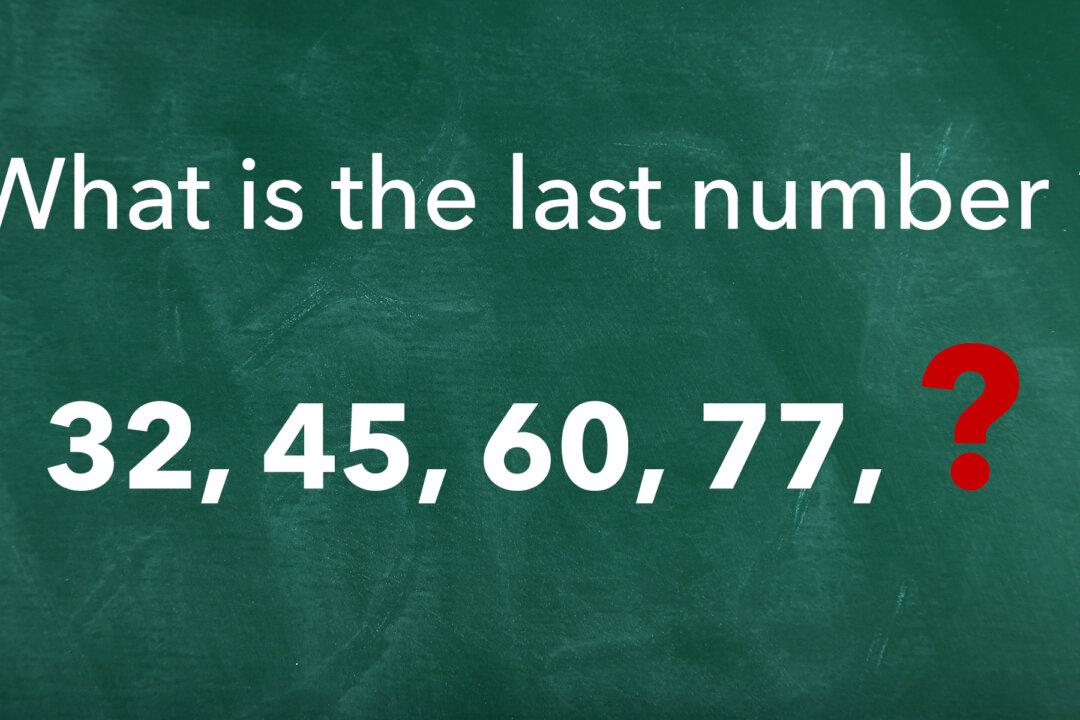For many people, middle school math problems are a distant memory of a time when we stared at the piece of paper with our pencils in hand, desperately trying to find some sort of order in an apparently random sequence of numbers.
While you might be eager to let the past be the past, especially where math is concerned, scientists say that keeping your brain sharp with number problems is a great way to fight dementia! So let’s take a walk down memory lane to the kind of math problem you might have encountered in middle school.